Week 2.1 - Sets

Sets

• Sets are a collection of 'things'.
  • Could be a collection of animals, people, or numbers.
  • It can also contain other sets.

• Our sets (mostly):
• (Subsets of) all natural numbers $\mathbb{N}$: 0, 1, 2, ...
• (Subsets of) all integers $\mathbb{Z}$: ..., -2, -1, 0, 1, 2, ...
• (Subsets of) all real numbers $\mathbb{R}$ (e.g: $\pi$, $e$, 3.14, ...).
• Empty set: $\emptyset$ (contains no elements inside)
• Sets containing lowercase letters representing "abstract" objects, e.g., ${a,b,c,x,y}$
• Set containing above sets as elements

Defining sets

• By enumeration (listing all members)

  • {dog, cat, elephant}
  • {1, 2, 3, 25, 72}
  • Note that the order and repetition are unimportant, i.e., {1, 2, 3} = {2, 1, 3} = {3, 2, 2, 3, 1}
  • Not convenient for very large or infinite sets

• Descriptively, through a property that identifies all its elements:

  • The set of all people in this classroom at this particular time.
  • We can make descriptions more precise by using a mathematical notation.

• We can make descriptions more precise by using a mathematical notation:

• $P(x)$ means that the (mathematical) object $x$ satisfies the property $P$.

• We write: $A = {x | P(x)}|$

Defining sets - examples

$S_n={x \mid x \in \mathbb{N} \text{ and } 1 \leq x \leq n}$

• $S_n$ is the set ${1,2, \ldots, n}$
  $B={x \mid x=3 n+2, n \in \mathbb{N} \text{ and } 1 \leq n \leq 4}$
• $B$ is the set ${5,8,11,14}$
  $\mathbb{N}^{+}={x \mid x \in \mathbb{Z} \text{ and } x>0}$
• $\mathbb{N}^{+}$is the set of positive integers
  $\mathbb{Q}={{\frac{x}{y} \mid x \in \mathbb{Z} \text { and } y \in \mathbb{N}^{+}} }$
• $\mathbb{Q}$ is the set of rational numbers (fractions)

Computational features of sets

• Set is an (abstract) data structure.
  • Data structures are mainly interesting in relation to the queries and operations that they support.
• Queries and Operations:
  • Membership, Containment/Subset, Equality, Cardinality, Power set, Union, Intersection, Complement, Cartesian Product, ...
• Which operations are supported in concrete implementation depends on the application.

Membership

• Given an object $a$ and a set $A$, does the object belong to the sets?

• We write: $a \in A$.

• We say: $a$ in an element of $A$.

• Examples:

  • $1 \in {1, 3, 7, 25}$
  • $a \notin {b, d, c}$ (not an element)
  • ${x, y} \in {b, {x, y}, , 13}$

• Exercise: True or False?

  • $3 \in \mathbb{N}$ True

Subsets

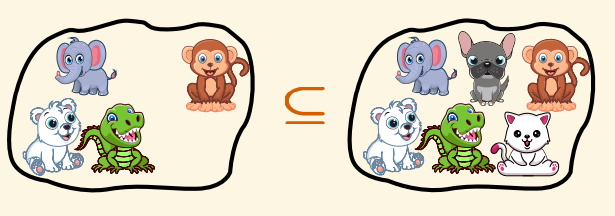
• We say: set $A$ is a subset of set $B$
• We write: $A \subseteq B$
• We mean: if $x \in A$, then $x \in B$ for any object $x$
• Examples:
  • ${25, 7} \subseteq {1, 3, 7, 25}$
  • ${a, c} \nsubseteq {b, d, c}$ (not a subset)
  • ${b, {x, y}} \subseteq {b, {x, y}, z, 13}$
  • ${a, 2, b, 25} \subseteq {a, 2, b, 25}$
  • $\emptyset \subseteq {a, 2, b, 25}$

Equality

• When are sets $A$ and $B$ the same - $A = B$?
  • When they have exactly the same elements.
• How do we check it?
  • If $A$ and $B$ are small -> check each element.
  • What if $A$ and $B$ are large or infinite?
    • We check that: $A \subseteq B$ and $B \subseteq A$.

Exercise:

• $A={x \mid x=2 n+1 \text{ for some } n \in \mathbb{Z}}$
• $B={y \mid y=2 m-3 \text{ for some } m \in \mathbb{Z}}$
• Step 1.: $A \subseteq B$
  • If $x \in A$, then $x=2 n+1$ for some $n \in \mathbb{Z}$.
  • Then, $x=2 n+(4-4)+1$.
  • So, $x=(2 n+4)+(-4+1)$.
  • Then, $x=2(n+2)-3$.
  • Therefore, $x=2 m-3$ where $m=n+2$ for some $n \in \mathbb{Z}$, so $m \in \mathbb{Z}$ and hence $x \in B$.

Cardinality

• How many elements are in the set?

• We say: The cardinality of the set $A$ is $n$.

• We write: $∣A∣ = n$

• We mean: The number of elements in the set $A$ is $n$

• Examples:

  • $|{1,3,7,25}|=4$
  • $|{b, d, c}|=3$
  • $|{{x, y}, z, 13}|=3$
  • $|\emptyset|=0$ (Emptyset has cardinality 0$)$
  • $|\mathbb{N}|=\infty$ (If $A$ is infinite set, we write $|A|=\infty$ )
  • How can we compare the cardinalities of two sets if they are infinite?

Power Sets

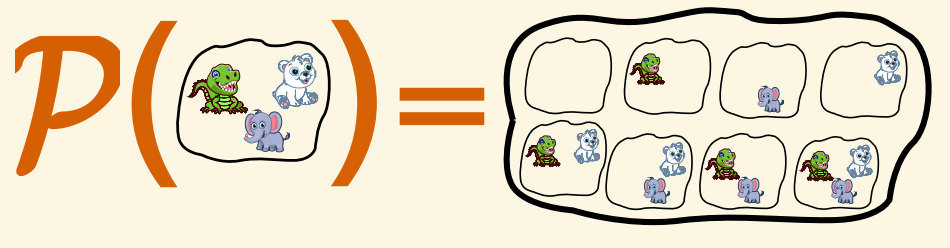
• The power set of set $A$ is the set containing all subsets of $A$.
• We write: $P(A) = {S ∣ S ⊆ A}$
• Sometimes we write $2^A$ instead of $P(A)$
• Example: $P({0, 1}) = {{\emptyset, {0}, {0, 1}}}$
• Facts for every set $A$:
  • $\emptyset \subseteq P(A)$
  • $A \subseteq P(A)$
  • $|P(A)| = 2^{|A|}$